Вычесть из смешанной обычную и наоборот

Как вычесть из смешанной обычную или наоборот, как вычитать из обычной смешанную. И последним пунктом разберем. как отнять от смешанной обычную на калькуляторе.

О вычитании обычной из смешанной

1. Правило вычитания обычной дроби из смешанной
2. Вычесть из смешанной обычную дробь с разными знаменателями
3. Правило вычитания смешанной дроби из обычной с примером
4. Как вычесть обычную дробь из смешанной на калькуляторе

Правило вычитания обычной дроби из смешанной

Рассмотрим два правила вычитания обычной дроби из смешанной :

Первое - классическое, которое написано в учебниках.

И второе - которым пользуюсь я(с использованием если).

Первое классическое Правило вычитания обычной дроби из смешанной

Чтобы вычесть из смешанной дроби обычную(без всяких если), превращаем смешанную в обычную
Отнимаем две дроби, как обычные дроби.
Поскольку числитель больше знаменателя, нужно из дроби выделить целое.

Выше приведенное правило можно и нужно использовать, но я пользуюсь другим, просто я так привык! Мне кажется, что так вычитать проще... с использованием если, как в программировании


Альтернативное правило вычитания обычной дроби из смешанной

Для того, чтобы вычесть из смешанной дроби обычную, нужно :

Если дроби имеют разные знаменатели, то приводим две дроби к общему знаменателю - наименьший общий знаменатель.

Если числитель смешанной дроби больше числителя обычной дроби, то отделяем целое и вычитаем две дроби ка обычные дроби, и далее возвращаем целое на место. Рассмотрим это на примере.


Если числитель обычной дроби больше числителя, смешанной дроби, то занимаем одну целую от целого смешанной дроби преобразовываем это целое в дробь и прибавляем к числителю смешанной дроби.. Теперь, мы можем вычесть из получившейся неправильной дроби - обычную.

Отнимаем от смешанной дроби обычную с одинаковыми знаменателями.

Возьмем первые две дроби, которые пришли на ум... будем отнимать от смешанной дроби одна целая три пятых и обычную две пятых

1|3/5 - 2/5

Первым пунктом исходя из альтернативного правила , сравниваем два знаменателя, как видим и в смешанной и в обычной, знаменатели одинаковые = 5. Первый пункт правил пропускам и переходим ко второму :

1|3/5 - 2/5

Вторым пунктом, проверяем числитель первой дроби и числитель второй дроби - здесь нам тоже ничего не нужно делать дополнительно! см.второй пункт правил.

1|3/5 - 2/5

И далее отделяем целое от смешанной дроби - отнимаем две дроби 3/5 и 2/5, как обычные дроби:

После действия вычитания возвращаем целое на место.

Результат вычитания из смешанной дроби обычную :

135 - 25 =

1 + (35 - 25) =

1 + (3 - 25) =

1 + (15) =

115



Вычесть из смешанной обычную дробь с разными знаменателями

Не будем использовать сложные примеры, нам ведь нужно, чтобы вы разобрались, а не сломали свой нежный мозг...



Возьмем дробь смешанную и правильную с разными знаменателями :

1|2/3 - 1/6

Как мы помним из альтернативного правила вычитания обычной из смешанной дроби -0 первым пунктом смотрим на знаменатели, они здесь разные 3 и 6, значит нам нужен наименьший общий знаменатель - раскладывать на множители не нужно, поскольку и так понятно, что общий знаменатель в данном случае будет равен - 6.

1|2/3 - 1/6

Отделяем целое 1 + (2/3 - 1/6)

Приводим к общему знаменателю первую дробь умножаем на 2(как я уже неоднократно говорил, что наверное знаете, что при умножении числителя и знаменателя на одно и тоже число - значение дроби не меняется!): 1 + (2*2/3*2 - 1/6) = 1 + (4/6 - 1/6).

Отнимаем числители 1 + ( (4 - 1)/6) = 1 + (3/6)

Смотрим на дробь, которая получилась, её можно сократить на 3. Числитель и знаменатель делятся на 3. 1 + (3:3/6:3) =1 + (1/2)

Возвращаем целое на место 1 + (1/2) = 1|1/2.

Результат вычитания из смешанной дроби обычную с разными знаменателями:

123 - 16 =

1 + (23 - 16) =

1 + (2*23*2 - 16) =

1 + (46 - 16) =

1 + (4 - 16) =

1 + (36) =

1 + (3 : 36 : 3) =

1 + (12) =

112



Правило вычитания смешанной дроби из обычной с примером

Для данного варианта не существует отдельного правила!

Для вычитания из обычной дроби смешанной, нужно воспользоваться классическим правилом вычитания смешанной дроби из обычной

Пример : как вычесть из обычной дроби смешанную с разными знаменателями

Чтобы не морщить лоб, возьмем пример из выше разобранной темы и поменяем смешанную и обычную дробь местами :

1/6 - 1|2/3

Данный пример будем считать по классическому правилу :

Приводим смешанную в обычную - 1|2/3 = 1*3/1*3 + 2/3 = 3/3 + 2/3 = 5/3.

Приводим к общему знаменателю - наименьший общий знаменатель - это 6. 5*2/3*2 = 10/6

Теперь отнимаем, как обычные дроби 1/6 - 10/6 = - 9/6

1/6 - 10/6 = (1 - 10)/6 = - 9/6

Сокращаем дробь

- 9 : 3/6 : 3 = -3/2 Выделяем целое
-3/2 = - 1|1/2

Результат вычитания из смешанной дроби обычную :

16 - 123 =

16 - (1*31*3 + 23) =

16 - (33 + 23) =

16 - (3 +23) =

16 - 53 =

16 - (5*23*2) =

16 - 106) =

1 - 106 =

- 96 =

- 9 : 36 : 3 =

- 32 =

- 112



Как вычесть обычную дробь из смешанной на калькуляторе

Для того, чтобы вычесть обычную дробь из смешанной на калькуляторе нужно уметь набирать дроби.

Для иллюстрации того, как можно вычесть обычную дробь из смешанной на калькуляторе, нам понадобится пример! Чтобы далеко не ходить, возьмем выше приведенный пример:

1|2/3 - 1/6

Набираем дробь - 1|2/3.

Нажимаем кнопку вычесть



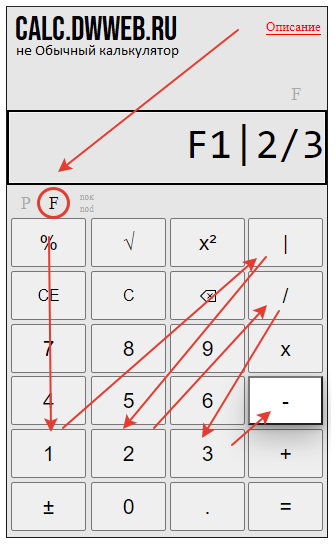
Набираем вторую дробь - 1/6.

Нажимаем кнопку равно :



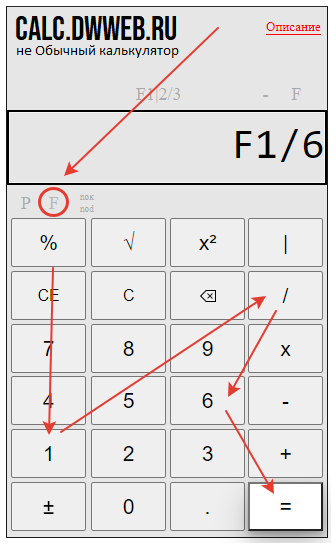
Получаем результат вычитания обычной дроби из смешанной на калькуляторе ^